2023 Vol. 15 №2

Evaluating the efficiency of the research sector in Russian regions: a dynamic data envelopment analysis

DOI

10.5922/2079-8555-2023-2-5

Pages

82-102

Abstract

The nonparametric method of dynamic data envelopment analysis (DDEA) has become increasingly popular for conducting comparative efficiency evaluations. In recent years,
dynamic data envelopment analysis (DDEA), a variant of this method, has gained significant attention. This article applies dynamic analysis to evaluate the efficiency of the research sector in Russian regions. Traditional input variables such as the number of research staff and R&D expenditure are considered, while publication and patent metrics serve as output indicators. The analysis covers a substantial time period, spanning from 2009 to 2020. Notably, the proposed evaluation method incorporates publication quality measures as a carry-over variable, in addition to accumulated R&D expenditure. The study employs dynamic data envelopment analysis to compare the obtained results with previous evaluations of the research and technology sector in Russian regions. The findings demonstrate that the proposed method serves as a valuable ranking technique, enhancing existing evaluations of regions’ research and technology potential in terms of efficiency. The article concludes by discussing the prospects and limitations of the method in evaluating and forecasting research and technology profiles of regions.

Reference

Introduction

Data envelopment analysis (DEA) spans a wide range of nonparametric methods routinely used for ranking study objects according to their production efficiency [1], [2], [3]. A comprehensive review of modern types of DEA is the work by Chiang Kao [4]. This widely used method continues to develop, which is especially true for its dynamic [5] and stochastic [6] applications. In Russian literature, the first studies into the use of DEA appeared at the turn of the 21st century [7], [8], [9]. Particularly, the method was employed in comparative efficiency assessments [10], [11], [12], [13], [14], [15], [16], [17].

DEA builds on the universal notion of efficiency defined as the ratio between outputs and inputs for a certain object. Since it does not presuppose functional dependence between inputs and outputs, this method can be classified as non-parametric. The principal tool of DEA is optimisation. The essence of the method is that it solves as many optimisation problems as there are objects of observation. Moreover, the objective function reflects in one form or another the efficiency of objects, one by one, whilst the system of constraints includes data on all the objects [18]. All the objects are optimally assessed using available data, and this makes it possible to compare the objects, ranking them according to their capacity to transform resources into results.

A strength of DEA is the possibility to include in the analysis several outputs varying in scale and units of measurement. This makes the method universal: the selection of study objects (for instance, regions) determines the disciplinary area, and the choice of resources and results (for example, research) determines the subject area of the analysis.

This study aims to create a new type of ranking for regional research, using dynamic DEA as a comparative efficiency assessment method.

DEA has gained wide acceptance in regional studies as a well-established research method for the multi-­factor comparison of regions [19]. It is also extensively used in assessing technological capabilities within selected industries [20], [21]. Following several earlier studies [22], [23], [24], [25], we employ DEA to assess the efficiency of regions in terms of research and technology. The two latter publications are based on Russian regional data allows comparing the findings.

We view DEA as an approach to evaluate the efficiency of objects’ performance, as we do regression analysis, the index method and stochastic production frontier analysis. The results of such evaluations, as a rule, underpin guidelines for increasing the efficiency of objects’ performance and help identify inefficient objects of systems at macro-, meso- and micro-­levels by building the so-called ‘efficient frontier’ determined by the performance of the most effective objects from the array. The method can also be employed in analysing the influence of various territory-­specific factors that are at odds with the characteristics of the regional system. For instance, this can be done to assess the efficiency of regional research and education systems [26], the energy sector [27], environmental management systems [28], and innovative production [29]. DEA does not focus on processes within the system but aids in analysing inputs and outputs, as well as providing recommendations on optimizing them to increase the system’s efficiency [30].

Using DEA to study the system of knowledge production offers helps make informed personnel and financial decisions at a regional level to ensure the efficiency of the innovative system. As mentioned above, the usual result of employing DEA is an analysis of deviations from the efficient frontier in the performance of some objects and recommendations for improving their efficiency.

Following the target-­setting method, Svetlana Ratner [31] proposes calculating projections for the inefficient objects of regional systems within the space of inputs and outputs on the efficiency frontier. This would make it possible to determine input reduction and output increase targets, thus ensuring the object’s efficiency. Window analysis has been employed for the dynamic assessment of objects’ efficiency. This method involves selecting an observation window of a certain length for each production facility, which ensures the robustness of efficiency assessment and reveals trends in efficiency. Olga Komarevtseva [32] uses DEA to assess the intensity of the link between the financial and social efficiency of municipalities in the Orel region. The methods can also be employed to assess the efficiency of organizations, using financial indicators of financial and economic performance rather than focusing solely on the amount of resources expended or outputs [33]. Aliya Alimkhanova and Artur Mitsel emphasise the applicability of DEA to assessing efficiency regardless of the combination of resources and rank objects according to efficiency. Therefore, inefficient objects can be identified and recommendations produced for improving their efficiency.

The method helps describe the states of efficiency and changes in it, which are not often predetermined by the amount of resources in regions. A great strength of DEA is that its results often challenge the stereotypes about how well regions can fare in research and technology. Yet, these results are to be taken with a grain of salt as they heavily depend on the quality of the data. For example, if regional statistics systematically misrepresent the amount of expenditure or personnel capacity in a region, the resultant assessment may be incorrect.

Overall, the methodological problems of DEA are a by-product of its advantages. Firstly, DEA is very sensitive to data quality, including outliers, sudden shifts, and other factors. Secondly, the traditional tools of statistical assessment of results are not applicable to the classical variation of DEA. However, the literature has described some approaches to address this problem (see [6]). Therefore, if it is necessary to take into account the randomness of data evaluation, alternative classes of models should be used such as stochastic frontier analysis (SFA; see [1], [34]).

The structure of this article takes the following form. It begins with a characteristic of the dynamic model employed, which builds on the ideas of Chen et al. developed in [22]. Then follows a description of data on research1 conducted in Russian regions in 2009—2020, which are used along with publishing performance data, 2008 internal R&D expenses figures and patent statistics since 2007. Further, cut-off values are given that were used when forming the final sample of regions. The next section contains the main results of the calculations and offers their visualisation, comparing them to earlier data. Discussion and conclusions round off the article.

Dynamic DEA model

DEA is used to assess efficiency defined as the ratio between effects (results) to resources expended. Within DEA, efficiency assumes, as a rule, the form of technical efficiency, i. e., the ratio between the optimal amount of necessary resources per unit of output and resources actually expended (for more detail, see [1]).

When using DEA, the optimisation problem can be viewed as the primal or dual problem, i. e. based on an envelope or a multiplier. We use a dynamic model [18], [22], which, in turn, is a modification of the relational analysis model proposed by Kao [18], who adheres to the multiplier form. And we will do the same.

So, n objects of observation (regions) are given, for which panel data have been collected for T periods and three groups of variables: inputs Yr, outputs Xi and carry-over (transitioning from one period to another), Zp. In the context of dynamic DEA, particular attention should be paid to carry-over variables Zp (Fig. 1) since, without them, the model would be a simple aggregate of T statical models.

1

The principal scheme of dynamic DEA (adopted from [22, p. 107])

The scheme considers one variable of each type for one object of observation. Extending this scheme to all the objects requires collating panel data, which will be described in the next section, carry-over variable should be collected for T + 1 periods.

Unfortunately, matrix notation is not suitable for the description of this problem, and thus the cumbersome index notation is used. The problem of maximising individual efficiency can be expressed as follows:

Optimisation occurs over positive multipliers ur, vi, wp, with ε being some small positive value. Looking ahead, we will consider six multipliers: two per each groups of variables. Optimisation will result in six sets of multipliers. Multipliers do not change across periods.

As can be seen, the maximum value of the objective function (the first expression, Ek) is the indicator of interest, i. e. that of the efficiency of some object k from a set n. The expression of the objective function differs from the first group of constraints (n each) only in that the index j replaces the index k, where j = 1, 2, ..., n. This means that we have to solve a separate problem form each k, with the restriction imposed that the efficiency of no object from the group can exceed one.<2>

Finally, there is the second group of n × T constraints. The expression for it differs from that for the previous one in that it lacks external summation over T (in our case, there will be 804 such constraints for each k). To ensure a more effi­cient numerical solution, the expressions in the model are modified in such a way as to remove cumbersome ratios (see [18, p. 327]). Since efficiency is a ratio, the denominator can be normalised to 1.

By expressing the numerators and denominators from the second group of constraints as B = ∑r = 1urYrj + ∑p = 1wpZpj and A = ∑i = 1vi Xij + ∑p = 1wpZpj, a simplified scheme of the problem can be written as follows<3>:

In this representation, summation is conducted over T and t-th indices are omitted for simplicity. This simplified scheme is implemented using the Wolfram functional programming (Appendix).

Data

We collected data on traditional indicators for research. The data on Russian regions are for 2008—2021, with the first and last periods reserved for averaging the research indicators and creating carry-over variables. Therefore, T = 12 in the model, i. e., it spans the period from 2009 to 2020.

As resource indicators, or inputs, we used statistical data found in the annual books Regiony Rossii. Sotsialno-­ekonomicheskie pokazateli [Russian regions. Socioeconomic indicators]:<4>

1. The number of R&D personnel. This metric covers various categories of people employed in the field rather than researchers only, since such an approach is more suitable for efficiency assessment.

2. Internal R&D expenses. All the evaluations, which are based on the regional consumer price index, are normalised to 2010 values.

Resulting indicators (outputs):

1. The number of publications covers research works of all types from the years 2010—2021, indexed in Scopus [5]. It is shifted one period forward since, by convention, there is a time lag of one to three years between expenditure and publication [35].

2. The number of patent applications filed. The statistics on Russian regions are according to Rospatent.<5> The values were averaged over three years as this metric is characterised by sudden annual shifts. In contrast with publication metrics, here we assume that patent applications are filed during its preparation period.<6>

The Scopus database by Elsevier was chosen as a source of bibliometric data. Publications’ metadata include the affiliation of all authors, making it possible to distribute the array of Russian publications by region. The data were aggregated for Russia’s 78 regions and federal cities.<7>

Aggregation was carried out using the full counting method [36]: a publication co-authored by researchers from different regions gives each region a credit. Thus, it was necessary, firstly, to include publications from organisations with a validated Scopus profile into a regional set and, secondly, to search for publications from organisations with such a profile and add them to the corresponding regional sets.

Finally, as carry-over variables, the model used:

— accumulated expenses calculated by aggregating the shares of internal R&D expenses in 2008—2020;

— Scopus field-­weighted citation impact (FWCI) of publications for 2009—2021. It is the ratio of citations to the expected worldwide average for the field, type and publication year.<8> A FWCI of 1 means that the citation impact of a work is exactly the global average. We smooth this metric for two consecutive periods.

It has been proposed in the literature to use variables associated with stocks, typically capital stocks, as carry-­overs. Statistics of this nature, as is known, are difficult to collect when it comes to research and technology. However, period-wise accumulated internal expenses seem to be a good proxy indicator [22]. In our model, we capitalise 5 % of such R&D expenses annually<9> and use a 20 % depreciation rate.

Citation impact gives insight into one of the aspects of academic publishing quality. We assume that research is closely bound up with the accumulation of experience, which in turn has a bearing on the quality of findings. The accumulated number of publications is, on the one hand, a result of research and, on the other, an input resource to obtain new research results. One of the indicators of academic publishing quality is the FWCI. The indicator is normalised in such a way as to not require taking logarithms.

Since regions differ in scale, it seems reasonable to take logarithms of the main variables to obtain comparable time series. Although the final rankings are different between initial and logarithmic data, the logarithmic expression gives a smoother picture with a smaller spread in efficiency by year.

Figure 2 shows smoothed indicators and their symbolic representations. As can be seen, it is impossible to make any conclusion by visual inspection alone. Moreover, there is more than one indicator for each period in the model. This calls for automatic evaluation methods, such as dynamic DEA; the next section will reveal the results of its application.

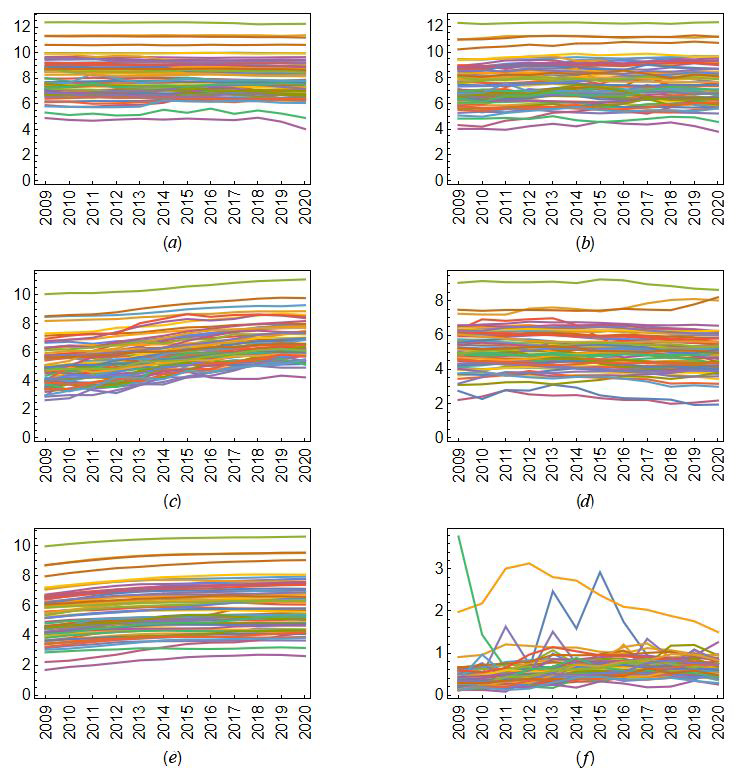
2

Changes in model data: a — the logarithm of R&D personnel number, X1; b — the logarithm of internal R&D expenses, X2; c — the logarithm of Scopus-­indexed publication number, Y1; d — the logarithm of three-year averaged number of patents, Y2; e — the logarithm of accumulated data at the end of a period, Z1; f — two-year averaged FWCI at the end of a period, Z2

Source: calculated by the authors based on data from Rosstat, Rospatent and Scopus.

Table 1 shows statistical characteristics of the data.

Comment: lagged series were used for carry-over variables

For the final ranking, regions with pronounced deviations in the data were excluded from the sample (for example, those with very low publication or patent activity).<10> The final number of regions was n = 67.

Results

In basic form, the solution of the optimisation problem, using a Mathemat­ic package, returns indicators of efficiency and corresponding overall ranking shown in Table 2. Columns 5 and 6 demonstrate, for reference purposes, ranking results obtained in earlier works [19], [25].

Comment: in column 5, the last two ranks were added because of the difference in the samples; in column 6, there are gaps in the ranks since our study covers fewer regions.

As Table 2 shows, the results of ranking by efficiency differ greatly from each other and those in column 6, which demonstrated innovation ranking results (19, p. 38—39). This might point to the fact that the link between capacity for innovation and efficiency is rather tenuous: indeed, the former does not necessarily entail the latter, and vice versa.

Figure 3 gives a visual representation of period-wise changes in efficiency. Despite the absence of a steady trend, the efficiency was in the range of 0.9 to 1.0, which is very much in line with the original study [22].

As can be seen, for a large group of regions, the indicator slightly decreased in the first half of the study decade, when the policy to encourage publication activities was introduced [37]. Later, the values grew slowly. The barely visible deceleration towards the end of the study period may be a result of the saturation and exhaustion of opportunities for the extensive growth of publication activities.

One of the most recent publications assessing the efficiency of the Russian region’s innovation systems is the contribution by Stepan Zemtsov and Maxim Kotsemir [25]. They examined the period between 1998 and 2012, which we consider only partially, and focused on assessing regional innovations and advances and technology, whilst we concentrate on research. These two areas, however, are closely linked and thus the findings of the two studies may prove comparable.

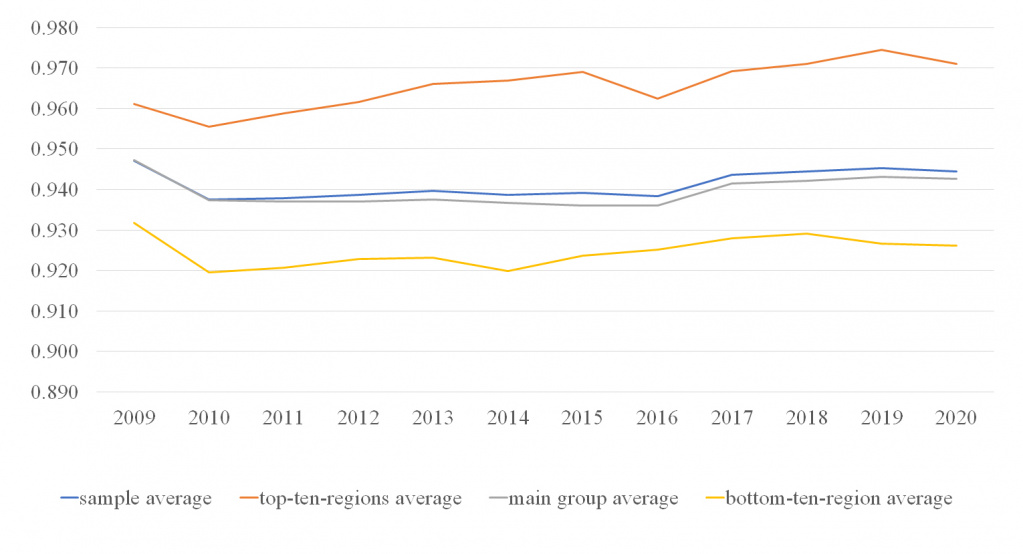
3

Changes in the calculated indicators over the study period (n = 67)

Overall, there is a statistically significant but weak correlation of 0.39 with the findings of Zemtsov and Kotsemir [25], which may be due to both differences in data and the peculiarities of DEA.

It is worth noting that our calculation has a smaller spread in efficiency values between regions: the difference is 10 %, whilst, the cited work reports an over 20-fold difference between the best and worst-­performing regions. Since we examine a narrower range of resources and only nonmonetary results, a slight difference in efficiency might be expected.

Another important difference is that, in the earlier work [25], Moscow is the leader by far, providing a benchmark for comparison. But, according to our calculations, Moscow is not the absolute leader in efficiency despite the considerable increase in publication activities observed over recent years. This decrease in Moscow’s relative efficiency is probably a result of its patent activity declining in the second half of the decade,<11> as well as of the capital accounting for the overwhelming proportion of research funding.

Discussion and conclusions

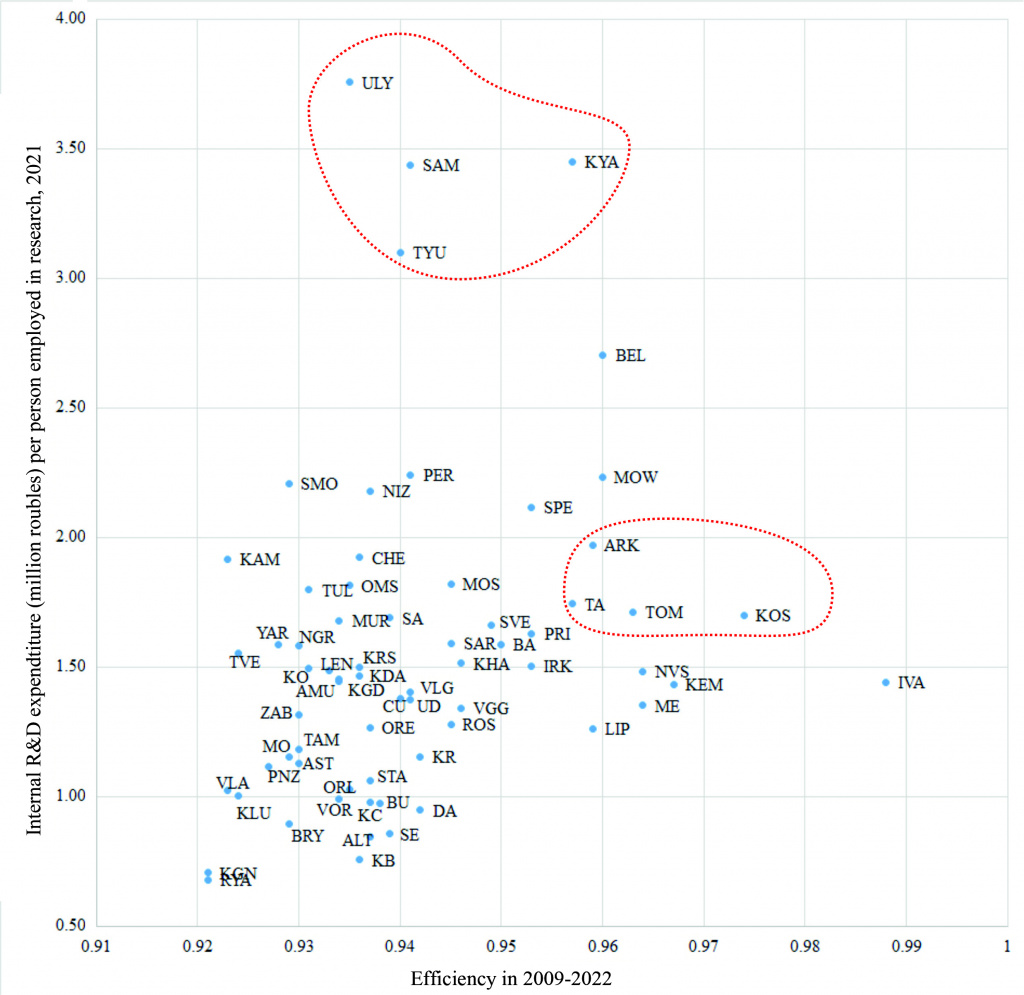
This study covers a relatively lengthy period, which is not common in the literature on dynamic DEA. As expected, the model is sensitive to the systematic underreporting of resource indicators at the data level. A prime example of this is the Ivanovo region, which typically scores low on resources but ranks high on research indicators.

As Figure 4 shows, the regions supersaturated with R&D financing have relatively low efficiency. These are the Ulyanovsk, Samara and Tyumen regions, and Krasnoyarsk Krai, well-resourced but far from excelling.

4

Correlation between R&D expenses and efficiency in Russian regions

On the other hand, Tomsk and Novosibirsk are ranked as leaders despite relatively generous funding. According to our calculation, Moscow is not the absolute leader, albeit ranked in top ten. This is yet another proof that efficiency is a relative indicator, and leadership in absolute values does not mean using the available resources to the fullest.

The opposite situation is also possible, especially when the resource allocation system overrelies on the ‘achievement principle’. For example, in the dynamic model (unlike the one described in [24]), the Kaliningrad region is ranked rather low in terms of research efficiency, despite a relatively high effectiveness growth rate.<12> This can be explained by the effect of the border region in a unique geopolitical position receiving substantial research funding.

On average, including in the model carry-over variables increases the efficiency indicators [22]: the distribution of indicators is comparable to that reported in the original study using our own and Kao’s methodology [18]. In Chen et al. [22], the overall efficiency is above 0.9 for all the study regions. In this study, period-wise results (the technical efficiency indicators) also vary between 0.9—1.0.

In general, dynamic DEA yields tangible results and is convenient to use. But we identified the model’s heightened sensitivity to expressing the indicators in the logarithmic form (see also [38]). It is also sensitive to changes in the expenses carry-over variable (in this case, it is a 5 % per cent share of internal R&D expense and 20 % depreciation). The model reacts less strongly to the quality variable of FWCI in the overall ranking (the citation impact mostly contributes to the accuracy of the efficiency indicator).

Dynamic DEA seems promising in assessing and comparing the efficiency of regional research. Yet, as in any other case, the ranking must be treated critically and the methodology supplemented with analytical statistics [19]. An important finding of this study is that capacity for innovation and efficiency may be weakly linked. Therefore, capacity-­based rankings should be supplemented with efficiency assessments, including those using DEA.

In further research, we will consider the possibility of comparing and combining the results obtained by different methods, such as SFA or the complexity index, in order to rank and cluster regions, using the collected data.

Appendix

Surprisingly, software implementations of dynamic DEA are rare despite the wide selection of libraries modelling static DEA. An exception is the library created based on [5].

We propose a short code implementation in the Mathematica package, whose functional programming and built-in optimisation functions seem to be adequate for solving the problem.

The minimum code necessary for solving the problem is neither optimised nor suited for scaling: rather, its purpose is to give an accurate picture of a simplified version of the problem.

Having initial data, it is possible to derive several variables:

VARS = {u1, u2, v1, v2, w1, w2};

{U1, U2, V1, V2, W1, W2} = ConstantArray[#, {n, T}] & /@ VARS;

OUT = U1 * Y1 + U2 * Y2 + W1 * Z1T + W2 * Z2T;

INS = V1 *X1 + V2 * X2 + W1 * Z1 + W2 * Z2;

VARS contains a list of symbolic variables for optimisation. The other rows include symbols for matrices of size n × T filled with symbols and data. U1, U2, V1, V2, W1, W2 are filled with symbols u1, u2, v1, v2, w1, w2 respectively.

Y1, Y2, X1, X2, Z1, Z2, Z1T, Z2T are filled with numerical values (data).

When forming OUT and INS matrices, the * operator means the element-wise product, i. e., Hadamard rather than the matrix product.

The main procedure is as follows:

NMaximize[

Flatten[{

Part[ (Total /@ OUT), #],

Part[ (Total /@ INS), #] == 1,

Thread[ (Total /@ OUT) < = (Total /@INS)],

Thread / @Thread[OUT < = INS],

Thread[ VARS > 0 ]

}],

VARS] & /@Range[n]

Let us comment on this procedure. In Mathematica, all expressions are contained in lists held by curly brackets {}. For example, the VARS variable includes a list of symbols. The matrix is a list comprising several other lists (rows). Functions take brackets []. Elements in lists and functions are separated by commas.

The notation (Total /@ OUT) for the OUT matrix means summation on rows (in effect, we apply the Total function to each row of the matrix; this operation is represented by an operator of the /@ form. Since OUT has size n × T, summation on rows is the summation over time. The same holds true for INS.

The Part[] function, as its name suggests, highlights a part of the list. For instance, the expression Part[ {a, b, c}, 2] will return the second value of b from the list {a, b, c}.

The Thread[] function is auxiliary. An example of the way it works is the expression Thread[VARS > 0], which would return the list of inequalities:

{u1 > 0, u2 > 0, v1 > 0, v2 > 0, w1 > 0, w2 > 0}.

As its name implies, this function ‘sews together’ lists of symbols making them lists of expressions. The Flatten[] function removes unnecessary brackets and forms a list with an objective function and constraints, a list that can be processed with the numerical optimisation procedure NMaximize.

Finally, the principal procedure NMaximize[ … # … ]&/@ Range[n] carries out numerical maximisation with respect to numbers from 1 to n, each number inserted instead of the symbol #. The # symbol stands for a pure variable, always accompanied by the symbol &. In this case, the values substituted for # form Range[]. For example, Range[4] will return a list with the values {1, 2, 3, 4}. Again, the operator /@ means that these values have to be substituted one by one but not all at once. This way, n optimisation problems are consecutively solved.

The results obtained through this procedure can usually be saved and worked upon later, but we leave this part out for concision. For more detail, see [39].